Python Graph Traversal Algorithms: DFS and BFS algorithms

Graph traversal (or graph search) is an important concept in computer science and programming. It refers to the process of visiting each node or vertex in a graph and checking or updating them. The algorithms that denote how this visitation are done are used to classify the type of traversal. I will be considering a python depth first search algorithm and a python breadth first search traversal of a graph in this post by applying them to finding the shortest path in a graph.

 

I believe that you are familiar with the graph classes I created in an earlier post. Because I will be using the objects of those classes as the model for the traversals we are going to be doing. If you are not familiar with the classes, I will encourage you to check the digraph and graph classes here. It only takes a minute or two.

Graph traversal has many applications in programming. It could be used to find all the nodes or vertices in a connected graph, find the shorted path between two nodes, test a graph for bipartiteness, or even analyse relationship and networks in a graph.

In this tutorial, we will be looking for the shortest path between two nodes using our algorithms.

The Python Depth First Search (DFS) traversal algorithm for shortest path in a graph

This depth first search algorithm requires that each node is called on exactly once for each connection on the graph. The algorithm is a recursive algorithm that ends when we find the end node in the path.

The search works by starting from a start node, and then it looks for all its adjacent nodes (i.e nodes connected by an edge), and it iterates through each of these nodes, also looking for their adjacent nodes recursively until it gets to a node without an adjacent node in the directed graph, or it gets to the end node. I modeled it as a directed graph because searching is directed in order to avoid cycles.

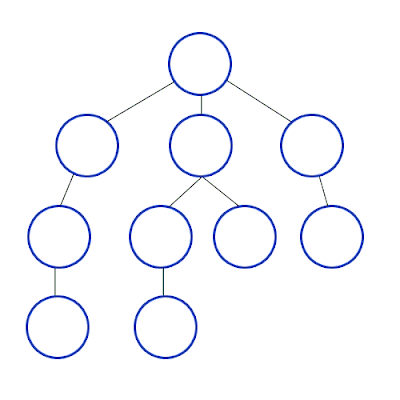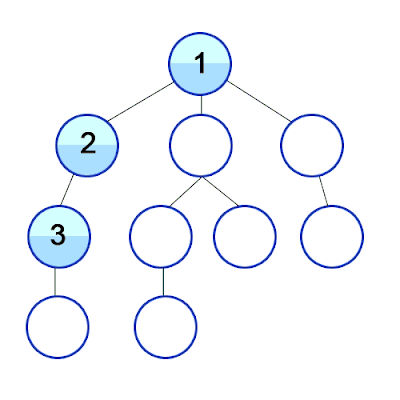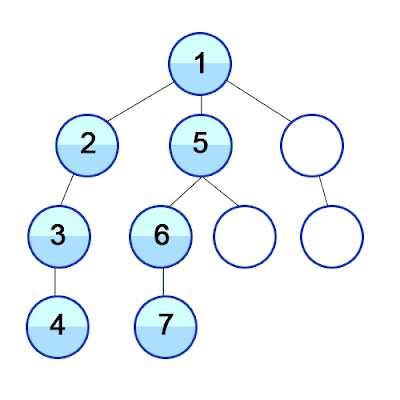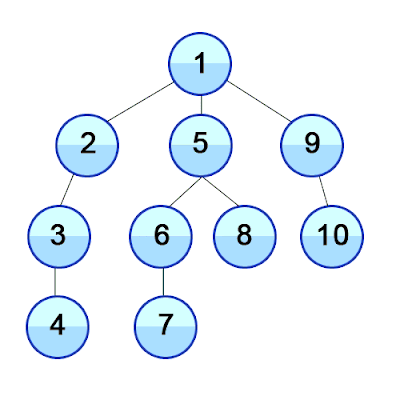
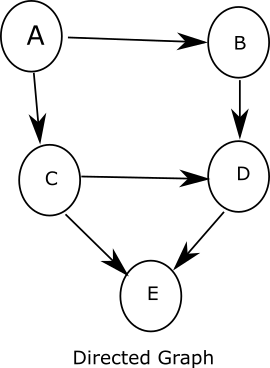
The graph below illustrates how graph search works in depth first search traversal. 

By Mre - Own work, CC BY-SA 3.0

Now, to implement the algorithm, we will be using the graph below. This is a directed graph with 5 nodes and 6 edges.

From the graph above, we will be taking a path from node A to node E.

You can run the code below to see how it works. The explanation of the relevant parts comes after. You can download the code for use on your machine at the last paragraph of this post.

If you read the code, you can see that the graph is modeled after the Digraph object, digraph, which explanation for the Digraph class is contained in the link I posted some paragraphs before this. The new parts of code that needs to be explained are the print_path function, the DFS function, and the driver code.

The code for the print_path function is found from lines 67 – 74.

    
def print_path(path):
    '''assumes path is a list of nodes'''
    result = ''
    for i in range(len(path)):
        result = result + str(path[i])
        if i != len(path) - 1:
            result = result + '-->'
    return result 

The code prints out each path or set of connected nodes while going through all the nodes in the graph searching for the end node. It uses a loop that iterates through the list of nodes in the path and concatenates each node with an arrow to represent relationship. It stores the name of each node in a variable, result, and prints out result at the end of the function.

The most interesting aspect of the code is the DFS function which does the actual python depth first search traversal. Here is the code from lines 76 to 90.

    
def DFS(graph, start, end, path, shortest, to_print = False):
    '''Assumes graph is a Digraph; start and end are nodes; 
    path and shortest are lists of nodes
    Returns a shortest path from start to end in graph '''
    path = path + [start]   #creation of visited nodes list
    if to_print:
        print('Current DFS Path:', print_path(path))
    if start == end:  # base case and end of the recurisve loop
        return path
    for node in graph.children_of(start):
        if node not in path:  #avoid cycles 
            if shortest == None or len(path) < len(shortest):
                new_path = DFS(graph, node, end, path, shortest, to_print)
                if new_path != None:
                    shortest = new_path

As you can see from the code above, the function, DFS, takes 6 arguments: the graph to search, the start and end nodes, the path of visited nodes, a shortest list of nodes that is the shortest path to the end node from the start node, and a keyword argument, to_print, that states whether you want a print out of the nodes as they are visited. The path argument refers to the visited nodes in the graph. We need to keep a count of visited nodes so that we don’t go through the same node more than once because that would mean going in a cycle. Then the shortest argument is the shortest path found so far starting from the start node. When we first called the DFS function, the shortest path was given the value None to indicate that we have not found a shortest path yet.

We indicated the base case for the recursive loop in an if statement that checks to see when the function is called recursively whether the start and end loops are the same. This makes sure the loop ends when we have arrived at the end loop and we can create the shortest path. This is indicated in lines 83 and 84. Then from lines 85 – 90, using a for loop when the traversal gets to each node we get the children of that node in the loop. First, we check to see whether that child has been visited before and if not we check to see if it will lead to the end node and if it does if the length from the start to that node is shorter than the shortest so far. If it is longer, we stop that search and go to the next child in the loop but if shorter, we recursively call the function again and where it returns a path to the end node, that becomes the shortest so far.

The function is guaranteed to return the shortest path if it exists.

Now, let’s go on to the second traversal algorithm, the python breadth first search (BFS) algorithm.

The Python Breadth First Search (BFS) traversal for shortest path in a graph.

Unlike in the DFS algorithm where we looked for the shortest path by first analyzing the child nodes, in the python BFS algorithm, we first explore the sibling nodes while looking for the shortest path. Sibling nodes are nodes with the same parent. We use a queue to understand which nodes have been visited and which has not been visited. The BFS algorithm guarantees that whenever it gets to the end node, that path discovered is the shortest path and other nodes do not need to be analyzed after that (unlike in DFS where you analyze every other node for length of path). Many programmers prefer to use the BFS algorithm for finding shortest path in a graph.

Now this is the code for the python BFS algorithm. Run it to see how it would work before I provide the explanation for new code. You can download the code for the python breadth first search (BFS) algorithm at the last paragraph of this post.

Other codes and functions are familiar except for the BFS function, so I will explain it in depth. The lines reference are from the embedded code above.

    
def BFS(graph, start, end, to_print = False):
    '''Assumes graph is a digraph; 
    start and end are nodes. 
    Returns a shortest path from start to end
    in graph '''
    init_path = [start]
    path_queue = [init_path] #store all the nodes currently being explored
    while len(path_queue) != 0:
        # get and remove oldest element in path_queue
        tmp_path = path_queue.pop(0)
        print('Current BFS path:', print_path(tmp_path))
        last_node = tmp_path[-1]
        if last_node == end:
            return tmp_path
        for next_node in graph.children_of(last_node):
            if next_node not in tmp_path:
                new_path = tmp_path + [next_node]
                path_queue.append(new_path)
        
    return None                     

The BFS function takes 4 arguments: the graph to be searched, the start and end nodes, and a keyword argument about whether to print out the visited nodes. On line 82 we create a queue of all the sibling nodes for each node that is currently being visited. This queue has the start node as its first node. On lines 88 and 89, we check if the last node in the current path being explored is the end node, if it is we have ended our search, but if it is not, then we move on to the next lines in the code.

On lines 90 – 93 we explore the child paths of the last node and add all the sibling nodes together to the path queue which will be explored in each iteration until we get to the end node.

Note that the BFS function returns the path from the start to end node if they are connected or if not, it returns None.

The DFS and BFS functions return the shortest path where they exist even while working differently. But the BFS is guaranteed to be faster in its implementation and does not go through needless iterations (unlike DFS) when the end node has been discovered because any path it finds to the end node promises to be the shortest path.

That’s it pythonistas. I hope you enjoyed my code for today. I had a swell time writing the code.

Drop a comment if you enjoyed it and say what you think needs to be changed. I would surely love to read your comments. Also, subscribe to my blog so you can receive regular updates when I post new articles. You can download the DFS code, depthfirstsearch.py and BFS codes, breadthfirstsearch.py, here.

Happy pythoning.

A Guide To Python Functions

When we write code we often have groups of related statements clustered together. It would be bad practice to continue repeating those statements. Good programmers group them together in a function. So, we will define our function as a group of related statements that perform a specific task.

 

Before we delve right into showing how functions are written in python, let’s explore the advantages of using functions in python.

Advantages of using python functions

Using functions rather than just clumping our code statements from line to line has several advantages. I will highlight three:

1.They make for code reuse – reusability.

Take for example we want to multiply a sequence of numbers 5,3, 4 etc. Writing code this way is foolhardy:

    
x = 5
y = 3
z = x * y
m = 4
n = z * m

It stresses the programmer’s resources. With a python function, we could do the multiplication any number of times with any number of objects. Like this:

    
def mult(x,y):
    return x * y

z = mult(5,3)
n = mult(z, 4)    

Code reuse becomes very important when we are dealing with a program that contains several lines of code. It would help for readability and understandability using a function.

2. They make the program manageable - modularity

Taking the example above. You could see that by breaking the statements into smaller chunks, we can manage the code. We could prevent the code from running off into several lines that would make a reader lost about the direction of the code.

When you have several functions working together, they exemplify the concept of decomposition in computer science. For example, for a laptop to function there are different parts. Take the screen, the keyboard, the charger, and the mouse as different parts exemplifying the functions of the laptop. When they work seamlessly, they achieve the idea of decomposition that makes functions a great idea for good programming practice.

3. It helps avoid errors in the code.

Using functions in coding can prevent errors, especially when you have several names that have to be defined. Python functions define their own namespace so that variables do not conflict with one another.

Now, how do you define a python function.

Python function definition.

The syntax for a python function is:

    
def function_name(parameters):
    ‘‘‘docstring’’’
    statement(s)
    return statement

The first line from the syntax above is called the function signature. The signature starts with the keyword ‘def’. The keyword ‘def’ tells the python interpreter that this is a function. Then next is the function name. The function name is unique to the function. You cannot start the function name with a number. It follows the rule of python as for writing identifiers. Then following it are the parameters of the function enclosed in parenthesis. Function parameters are the arguments the function accepts. We have discussed function parameters and arguments in another post. Following the function signature is the block of code that defines the body of the function. A colon ‘:’ is used to separate the signature from the body of the function.

The body of the function consists of docstrings which represent the documentation of the function followed by the statements that the function has to execute. Note that the documentation or docstrings are optional but it is good programming practice to include them in your functions. The documentation is enclosed by three quotation marks. Then the statements to be executed comes after the documentation. The last statement in your function should be an optional return statement. This ends execution of the function. Note that the return statement can occur anywhere in the body of the function but is usually found at the end and when they occur the function stops execution and control transfers to the caller of the function.

The function’s docstrings are a great idea for abstraction. That means, using the docstrings alone, you do not need to know how a function works to use it. The documentation or docstrings tells you what it does and it guarantees you that it works as the author states it.

When a function does not have a return statement, then that function returns None.

Let’s look at a typical function that includes all the syntax for a function. The docstrings or documentation in the function below explains what the function does.

    
def count(data, target):
    ''' Counts the number of occurrences of target
    value within data, an iterable
    Returns the number of occurrences as an int '''
    n = 0
    for item in data:
        if item == target: # found a match
            n += 1
    return n

The code above illustrates the typical features that can be found in a function.

Let’s look at another example that shows that a return statement can be placed anywhere in the body of a function but when it is encountered, it automatically returns control to the caller of the function.

In this contrived example, you can see that if the user enters Michael, the function ends at the return statement on line 7 but if some other name is entered, the return statement at line 9 ends the function and returns control to the caller of the function which is the print statement on line 12.

Now we have been talking about the caller of a function. Let’s us define how to call a function.

How to call a function.

The three ways you can call a function is either from the python prompt, from another function, or from within the program. To call a function, you write the name of the function followed by the parameters that you are passing to the function.

I will show examples where you can call a function from another function and within the program. They also apply to the python prompt.

a. From within the program.

In the function, mult, above we called the function on line 4 when the name of the function was used and then the parameters we want to pass to it were included in parentheses. Note that the parameters must correspond to the arguments of the function in the function signature. For a refresher on function arguments, you can see this post on positional and keyword arguments in python functions.

b. From within another function.

Functions are first-class citizens in python so you can call them from within another function. They can also be parameters to another function.

Take this example of a function calling other functions. Run it to see how it works.

The third function calls on the first and second functions to print their statements.

Also, see how the enter_name function below uses another function, print_name, as its argument or parameter, and then in its body it calls the function that was passed as an argument. The f formal argument is bound to the print_name actual argument that was passed when the enter_name function was called.

The function, enter_name, accepts another function as argument which was passed to it on line 8. It then calls the function in its body and that function when called prints out its statement.

These shows that functions are first class citizens and you can call them from even another function, and not only from within the program.

Variable scope and lifetime in functions.

The scope of a variable can be defined as the portion of a program where the variable is recognized. When a function is entered, the python interpreter creates a new scope or environment which contains the variables that the function recognizes. When a scope is created, names are being mapped to their values. Some of the variables that are scoped on function call are the parameters that are passed to the function. When the function is defined the parameters are called its formal parameters and when the function is called, the parameters are called actual parameters. When the function is called, a new scope is produced where the formal parameters are bound to the values of the actual parameters within the function namespace.

Also, other variables that are scoped in the function are any variables that are declared inside the function.

Take the following code for example:

    
def mult(x,y):
    ''' Returns the multiplication
    of its arguments, x and y, 
    where x and y are ints '''
    z = x * y
    return z

n = mult(2,3)    

When the function, mult, is called at the last line, python creates a new environment or scope for the variables that are recognized within the python function. First, it recognizes the formal parameters, x and y. It then binds x to its corresponding actual parameter, 2, and binds y to its corresponding actual parameter, 3. It then recognizes z that is declared within the python function. It multiplies the numbers and binds z to the value of the multiplication. So, we have 3 variables scoped within the function: x, y and z namely.

The variable n is outside the scope of the function and is said to be in a global scope.

Note that all the variables that are scoped in a function exists as long as the function is running. When the function stops running or returns, python garbage collects all the variables scoped within that function.

To see how this garbage collection of variables is done, let’s take an example.

You can see that the x in the function scope is now 30 when you run it, but the x variable in the global scope is still unchanged at 5. This is because when the function was exited the x in the function scope was destroyed and ceased to exist except for the x variable in the global scope. That shows you that the lifetime of variables in a function’s scope are for as long as the function is still running. Take note of that although there is an exception - functions defined as python generators which yield values. The following blog post explains python generator functions where the variables within its scope are not garbage collected.

One other point I want you to note about scopes is that even if a variable is not scoped within a function, that variable can still be accessed from inside the function but it cannot be modified from within the function.

Example: Global variables, x and y, accessed from within the function, mult.

Next example: We would have an UnboundLocalError if I try to modify either x or y without scoping them to mult.

I hope you now have all it takes to start writing your own functions in python and experiment with its powerful capabilities.

Happy pythoning.

Understanding and Converting File Sizes (Bytes, KB, MB, GB, PB)

Most times we want to understand what file sizes our data has. For example, when the file sizes are stated in bytes, we would want to understand what are the stated unit is in kilobytes, or gigabytes etc. Well, this can easily be coded in python.

 

But first, what are file sizes?

A Files size is a measure of how much data a computer file contains, or alternatively, the measure of the storage in memory it consumes. All file size units have the byte as the unit of measurement and all other units are derived from the byte.

A byte is a sequence of 8 bits processed as a single unit of information. A byte is enough to represent one unit of information. A bit is either an ‘on’ or ‘off’ position in the computer memory where “on” is represented by a ‘1’ and an “off” as ‘0’. So a byte contains 8 of such 1s and 0s. The computer processes our information as bytes.

In python, characters in strings are stored as one byte although extra bytes are allocated for storing any character so if you call sys.getsizeof(char) you may get more than one byte.

Larger bytes can be subdivided further into kilobytes, megabytes, gigabytes, terabytes, petabytes etc. The table below shows the different file units and their comparisons.

1024 bytes	1 KB
1024 KB	1 MB
1024 MB	1 GB
1024 GB	1 TB
1024 TB	1 PB

Where KB means kilobytes, MB means megabytes, GB means gigabytes, TB means terabytes and PB means petabytes.

Using the metrics above, given any number of bytes we can convert to other metric units.

I wrote a little program below that does just that. Given any number of bytes, it can convert the byte measure into larger sizes provided it is possible.

I hope you do enjoy it. I wrote it based on a request from a friend.

Happy pythoning.